Calculate required borehole depth

Calculating the required borehole depth is one of the most essential methods within the domain of borefield design. In this article, we will give you an overview of the different methods that are available in literature and we will discuss their advantages and disadvantages.

Calculate the required borehole depth

Conceptually, calculating the required borehole depth is relatively straightforward. The process begins with a selected borefield configuration and an initial guess for the borehole depth. The corresponding temperature profile is then calculated.

• If the average fluid temperatures remain within the defined temperature thresholds, the borefield is considered correctly sized.
• If the temperatures exceed these limits, the borehole depth is increased incrementally, and the temperature profile is re-evaluated.

This process is repeated until the system converges to a borehole depth at which the temperatures consistently stay within the specified bounds.

!Caution
In some cases, no depth will satisfy the temperature requirements, regardless of how deep you go. When this happens, an error will be returned. This situation, along with possible solutions, will be discussed in detail in a follow-up article.

Return to the borefield quadrants

In a previous article, the concept of borefield quadrants was introduced. (If you haven’t read this article, you can find it here.) It was stated that every borefield you encounter can be categorised into four quadrants based on two parameters: whether it is limited by the minimum or maximum fluid temperature and whether that limitation occurs in the first or last year of the simulation period.

When sizing the required borehole depth, you don’t know a priori which quadrant will result in the most critical design. One might argue that you should size the borefield once for each quadrant and then take the largest borehole depth as the critical design, which would give you four sizings per borefield. However, Peere et al. (2021) described that the same accuracy can be achieved by using only two sizings.

Imagine you size the borefield in quadrant 1 and then size it for the last year based on the maximum average fluid temperature. This will yield a temperature profile where the penultimate year exceeds the threshold slightly due to the imbalance, as do the preceding years up to the first year. Thus, the sizing in the first year (for the maximum average fluid temperature) will always result in a larger required depth than the sizing in the last year for that particular borefield and load.

Similarly, such a borefield will never be limited by quadrant 3, because when it is sized for the minimum average fluid temperature in the first year of the simulation, the temperature in the second year will be even lower due to the imbalance. Therefore, quadrant 4 will, in this case, always yield a larger borefield size than quadrant 3.

Due to the imbalance, you only need to check either quadrant 1 and 4 (in the case of an extraction-dominated borefield) or quadrant 2 and 3 (in the case of an injection-dominated borefield) when calculating the required depth. The resulting borehole depth is then equal to the maximum of these two values.

!Note
When taking the larger borefield size from the two relevant quadrants, it is important to always verify whether the maximum average fluid temperature is not exceeded. If this temperature threshold is crossed, it means there is no feasible solution for the given configuration and load. This situation and how to deal with it will be discussed in more detail in a future article.

5 different levels

In the literature, a wide variety of borefield sizing methods can be found, each with its own level of accuracy, speed, and complexity. In his PhD thesis, Ahmadfard introduced a framework that classifies these methods into five distinct levels, ranging from simple rules of thumb to detailed hourly simulations.

Below, each of these five levels is described in more detail, giving you an overview of the available methods and when they might be appropriate to use.

Level 0 – rule of thumb

The most basic level of borefield sizing relies on simple linear relationships between the peak thermal power and the total borehole length. These are often referred to as rules of thumb, typically expressed in the form of x W/m.

Although very easy to use, these methods neglect many important aspects of the design, such as the borefield configuration, borehole depth, ground thermal properties, thermal imbalance, and borehole thermal resistance. They also ignore seasonal and long-term thermal effects.

Because they are not based on any underlying physics, these rules of thumb can result in very high inaccuracies. Over- or undersizing by a factor of up to two is not uncommon. For that reason, this method should be avoided for actual sizing purposes and used only for the roughest early-stage estimates.

(More details can be found in our article on borefield design software).

Level 1 – constant load

The first level assumes a constant load on the borefield throughout the entire simulation period. This constant load corresponds to the annual thermal imbalance, evenly distributed over the 8760 hours in a year. Using this approach, the borehole-to-borehole thermal interaction—described by the g-functions (as explained in our article here)—can be taken into account. This immediately makes the method far more accurate than the rule of thumb sizing, since it allows different ground properties, configurations, and depths to be compared.

When visualised, the resulting temperature profile would resemble the figure below, where the characteristic curve of the g-function becomes visible.

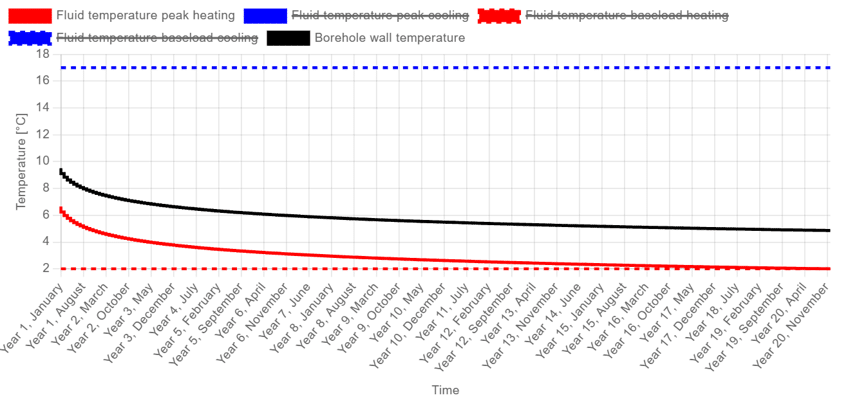
Although this method represents the long-term effects of the borefield fairly well, it does not account for monthly variations, peak loads, or the behaviour in the first year of operation. These elements are introduced in the level 2 methods and beyond.

Level 2 – three-pulse method

The three-pulse method, also known as the ASHRAE sizing method, is the most traditional approach for calculating the required borehole depth. It builds on the level 1 method by adding two additional heat pulses: one to account for the peak power and another for the energy exchanged with the ground during the month in which this peak occurs.

These three pulses—representing the imbalance, the monthly load, and the peak power—collectively capture both the long-term and short-term thermal effects of the borefield, resulting in a relatively accurate estimation of the required borehole depth. A graphical representation of this approach is shown in the figure below.

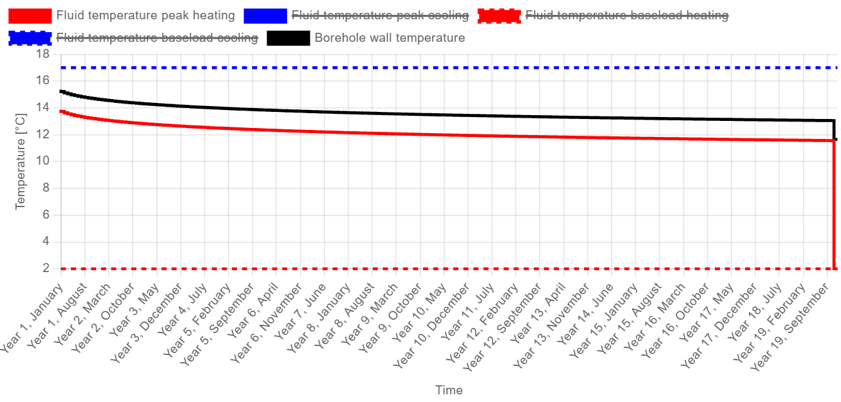
In the figure, the three distinct pulses are clearly visible. First, there is a long-term temperature trend similar to the one produced by the level 1 method, representing the effect of the annual imbalance. Then, a sudden drop appears due to the energy exchanged during the critical month (monthly load), followed by an even sharper drop in fluid temperature caused by the peak extraction event.

This method does not account for monthly variations in the load profile, a level of detail that is introduced in the level 3 sizing method.

!Note
This method is implemented in GHEtool’s back-end, but not directly available in GHEtool Cloud. It is considered less accurate than the level 3 sizing method, while only offering a slight improvement in computational speed. However, for applications requiring millions of sizing calculations—such as parametric studies or optimisation processes—the three-pulse method can be advantageous.

Level 3 – monthly resolution

Calculating the required borehole depth with a monthly resolution is the most common approach when using GHEtool Cloud, particularly in cases where only limited data is available. This method includes the same elements as previous levels—such as peak powers, long-term ground interaction, and ground properties—but also incorporates monthly variations in the load profile.

This results in higher accuracy, as it accounts for seasonal thermal energy storage, meaning the seasonal variation in borehole wall temperatures is now reflected in the sizing. A typical temperature profile calculated with this method shows this seasonal fluctuation clearly.

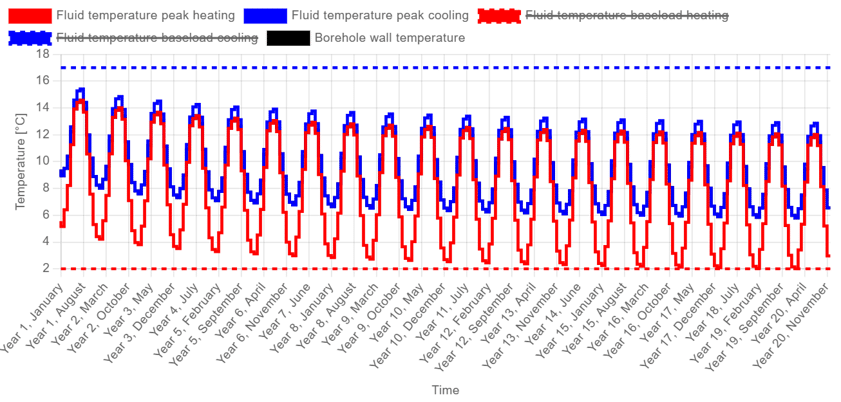
An important parameter in the level 3 method is the duration of the peak power. Depending on the building type and its emission system, this duration typically ranges between 6 and 12 hours, though longer durations are also possible. This assumption, however, is no longer required when moving to a level 4 sizing.

!Note
This method is fully implemented in GHEtool Cloud, offering a good balance between accuracy and computational efficiency, making it the preferred method for most practical applications.

Level 4 – hourly resolution

The most advanced method for calculating the required borehole depth is the level 4 method. Unlike the level 3 method, which works with monthly resolution, the level 4 method uses hourly input data. The key advantage of this approach is that the final assumption—regarding the duration of the peak power—is no longer necessary, as this information is directly extracted from the hourly profile itself. When hourly data is available, the level 4 method is the most accurate way to determine the required borehole depth.

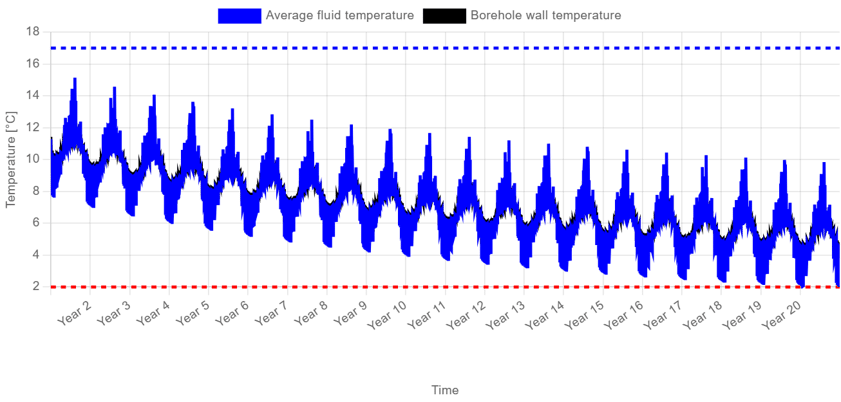
!Note
As discussed in the article on short-term effects (which you can find here), the current models do not yet include the thermal inertia of the fluid and the grout. As a result, the calculated fluid temperatures (shown in the example temperature profiles) tend to overestimate the real values, especially during sudden peaks.

We are currently working together with KU Leuven to develop a more refined model that accounts for these short-term dynamics. Once implemented, the level 4 method will become even more accurate and robust for advanced borefield design.

Conclusion

The article above described the various methodologies found in the literature for calculating the required borehole depth. These methods range from simple rules of thumb to detailed hourly simulations. Within GHEtool Cloud, the two most accurate methods—monthly (level 3) and hourly (level 4) calculations—are implemented, providing users with both precision and flexibility depending on the available input data.

In a next article, we’ll walk through a practical example showing how to use these methods for your own project. We’ll also explain how to interpret the gradient error, an important parameter that helps you evaluate the reliability of your borefield sizing results.

References

• Watch our video explanation over on our YouTube page by clicking here.
• Peere, W., Picard, D., Cupeiro Figueroa, I., Boydens, W., and Helsen, L. (2021). Validated combined first and last year borefield sizing methodology. In Proceedings of International Building Simulation Conference 2021. Brugge (Belgium), 1-3 September 2021. https://doi.org/10.26868/25222708.2021.30180
• Ahmadfard, M. (2018). A Comprehensive Review of Vertical Ground Heat Exchangers Sizing Models With Suggested Improvements. Thèse de doctorat, École Polytechnique de Montréal. https://publications.polymtl.ca/3034/